Manövrierfähigkeit nennt man die Möglichkeiten von Flugkörpern, ihre Lage im Raum sowie die Geschwindigkeit nach Betrag und Richtung zu ändern.
Manöver auf geradlinigen Bahnen sind Veränderungen des Betrages der Geschwindigkeit, zu den Manövern auf krummlinigen Flugbahnen gehören alle Kunstflugfiguren.
Bei der Beurteilung der Manövrierfähikeit von Flugzeugen kommt man um die Einbeziehung von Triebwerkskenngrößen nicht drumherum.
Für den gleichförmigen Horizontalflug (Geschwindigkeit und Höhe bleiben gleich) gilt:
Auftrieb = Gewicht (FA = FG) (Höhe konstant)
Schub = Widerstand (FS = FW) (Geschwindigkeit konstant)
Für jeden Flugzustand gibt es also einen erforderlichen Auftrieb und einen erforderlichen Schub (FS,erf).
Die Triebwerke liefern aber einen größeren als den erforderlichen Schub.
Diese Differenz zwischen erforderlichen und verfügbaren Schub (FS,verf) ist der Schubüberschuss, den man zum Beschleunigen aber auch zum Manövrieren nutzen kann.
Da in Kurven auf Grund des größeren Anstellwinkels ein größerer Widerstand überwunden werden muss, benötigt man mehr Schub – je größer die Schräglage, desto größer der erforderliche Schub.
Daraus ergibt sich die Tatsache, dass Flugzeuge umso besser manövrieren können, je größer der Schubüberschuss ist.
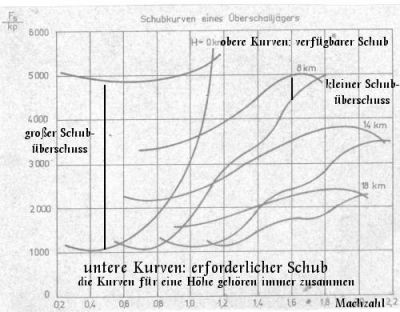
- für jede Flughöhe existiert ein Paar Schubkurven (je eine für FS,erf und FS,verf
- Die Differenz zwischen FS,erf und FS,verf (der Schubüberschuss) wird mit zunehmender Machzahl geringer
- es existiert also für jede Höhe eine Machzahl, bei der der Schubüberschuss am größten ist. Das ist die Geschwindigkeit, bei der das Flugzeug am besten manövrieren kann (größtes Dauerlastvielfaches, beste Längsbeschleunigung)
- im Schnittpunkt FS,erf und FS,verf ist die Maximalgeschwindigkeit erreicht (wenn sie nicht durch Betriebsbegrenzungen bei kleineren Werten festgeschrieben wird)
Dauerlastvielfaches:
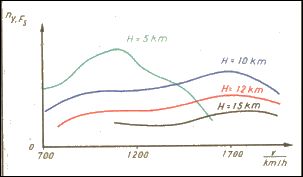
Von großer Bedeutung für die Beurteilung der Manövrierfähigkeit und damit das Verhalten des Flugzeuges im Luftkampf ist die Beantwortung der Frage, welche normalen Lastvielfache ny der Bedingung entsprechen, dass der verfügbare Schub (FS,verf) gerade den Widerstand ausgleicht, also gleich dem erforderlichen Schub (FS,erf) ist. Unter dieser Bedingung können in horizontaler Ebene noch Richtungsmanöver ohne Geschwindigkeitsverlust geflogen werden und bei Manövern im Raum kann von der Gültigkeit des Satzes der Erhaltung der mechanischen Energie ausgegangen werden.Daraus ist zu erkennen, dass mit zunehmender Höhe das verfügbare Dauerlastvielfache abnimmt, sich aber die Spitzen weiter in den Bereich großer M-Zahlen bewegen.
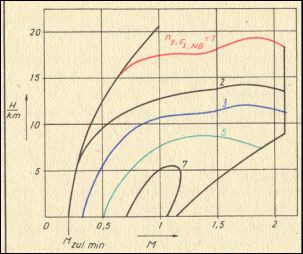
Diese Kurvenschar wird links begrenzt durch die Minimale M-Zahl, die das Flugzeug auf Grund seiner aerodynamischen Auslegung fliegen kann, rechts begrenzt durch die maximal mögliche M-Zahl.
Dazwischen liegt der fliegbare Bereich mit seinen möglichen Lastvielfachen.
Steigflugprofile:
Aus den Schubkurven und den damit verbundenen aerodynamischen Kenngrößen lassen sich auch bestimmte Flugregime ableiten, etwa das günstigste Steigprofil, um bestimmte Höhen zu erreichen. Dies soll einerseits sicherstellen, dass man in kürzester Zeit die befohlene oder gewünschte Höhe erreicht, andererseits aber nicht zuviel Kraftstoff durch den Einsatz des Nachbrenners „verpulvert“.Das Bild rechts zeigt typische Steigflugprogramme für das Flugzeug MiG-21 für den Steigflug mit und ohne Nachbrenner.
Schauen wir uns die Programme etwas genauer an:
Weiter oben haben wir uns ja schon mit den Schubkurven beschäftigt und herausgefunden, dass im Bereich des größten Schubüberschusses die Längsbeschleunigung am größten und damit auch das Steigvermögen am besten ist.
Für die MiG-21 ist die beste Steiggeschwindigkeit im Bereich von VW = 850-900 km/h. Dies ist die Geschwindigkeit, bei der im gefragten Höhenbereich bis ca. 10.000 m das beste Steigen erreicht wird.
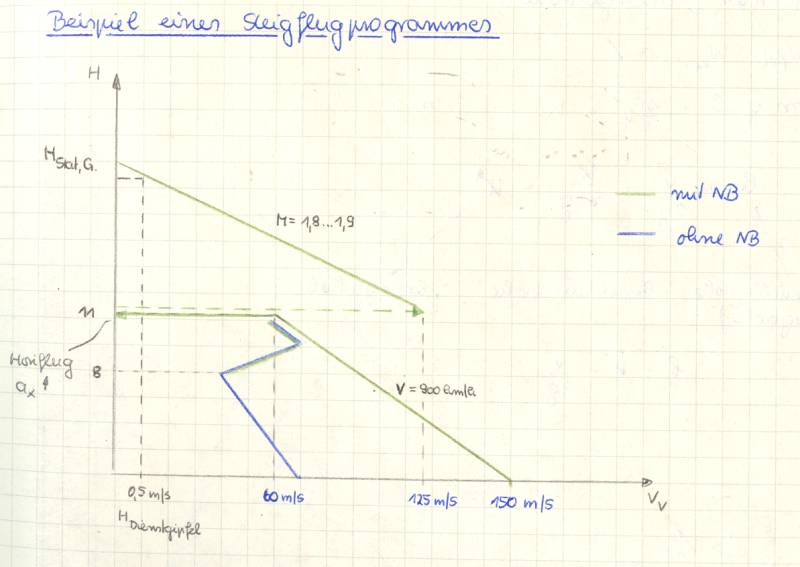
Flug ohne Nachbrenner: Nach dem Start, dem Einfahren des Fahrwerks und der Landeklappen wird demzufolge eine VW = 850-900 km/h eingenommen. Ohne den Einsatz des Nachbrenners stellen sich dabei Steigraten (je nach Triebwerk) von ca. 60 m/s ein. Mit zunehmender Höhe nimmt dieser Wert ab. Im Bereich der Tropopause (Temperatur ca. -53°C) steigt der verfügbare Schub des Triebwerkes nochmal an und die Steigrate wird wieder etwas größer. Ab einer Höhe von ca. 11.000m ist es aerodynamisch sinnvoller nach Machzahlen zu fliegen. Deshalb holt man in dieser Höhe im Horizontalflug eine Machzahl von ca. M = 1,8 – 1,9 auf (natürlich dann mit Nachbrenner) und erreicht mit diesen M-Zahlen wieder Steigwerte von über 100 m/s. Bei Einhalten dieser Werte ist das Erreichen der statischen Gipfelhöhe (das Flugzeug steigt noch mit 0,5 m/s) in der kürzesten Zeit möglich.
Dieses Steigflugprogramm ist ein Mittelwert zwischen günstigem Kraftstoffverbrauch und geringer Dauer.
Flug mit Nachbrenner: Um die zeitlichen Möglichkeiten voll auszuschöpfen ist ein durchgängiger Steigflug mit Nachbrenner möglich. Dabei liegen die Anfangswerte der Steiggeschwindigkeit in unteren Höhen im Bereich von 150 m/s . Auch hier wird in ca. 11.000m die Geschwindigkeit auf M = 1,8 – 1,9 erhöht und damit der Steigflug fortgesetzt.
Die geringste Höhe, in der im Luftraum der DDR mit Überschallgeschwindigkeit geflogen werden durfte, war 10.650m nach Standarddruck. Bei Flügen in die Stratosphäre wurde bis in diese Höhe mit Maximalleistung und VW = 850 km/h gestiegen. In 10.650 m Höhe wurde durch Einschalten des Nachbrenners und leichten Sinkflug (um das Ganze zu beschleunigen) Überschall aufgeholt. Bei einer M-Zahl von 1,4 – 1,5 wurde dann der Steigflug fortgesetzt (Für höhere M-Zahlen fehlte die Zeit, der Kraftstoff und die Notwendigkeit).